The observed behavior known as 1/f noise seems to show up everywhere. They call it 1/f noise (also known as flicker or pink noise) because it follows an inverse power law in its frequency spectrum. It shows up both in microelectronic devices as well as emanating from deep space. Its ubiquity gives it an air of mystery and the physicist Bak tried to explain it in terms of self-organized critical phenomena. No need for that level of contrivance, as ordinary entropic disorder will work just as well.
That as an introduction, I have a pretty simple explanation for the frequency spectrum based on a couple of maximum entropy ideas.
The first relates to the origin of the power law in the frequency spectrum.
Something called random telegraph noise (RTS) (or burst or popcorn noise) can occur for a memory-less process. One can describe RTS by simply invoking a square-wave that has a probability of B to switch states at any dt time interval. This turns into a temporal Markov Chain kind of behavior and the typical noise measurement looks like the following monkeys-typing-at-a-telegraph trace and sounds like popcorn popping in its randomness. It pretty much describes an ordinary Poisson process.
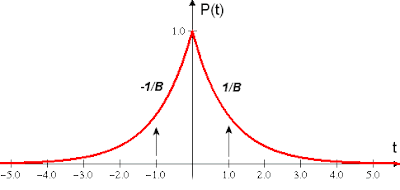 The autocorrelation (or self convolution) of a stochastic statistical has some interesting properties. In this case, it does have maximum entropy content for the two-sided mean of 1/B -- MaxEnt for the positive axis and MaxEnt for the negative axis.
The autocorrelation (or self convolution) of a stochastic statistical has some interesting properties. In this case, it does have maximum entropy content for the two-sided mean of 1/B -- MaxEnt for the positive axis and MaxEnt for the negative axis.In addition, the Fourier Transform of the autocorrelation gives precisely the frequency power spectrum. This comes out proportionately to:
S(w) = sqrt(2/π) / (B2+w2)where w is the angular frequency. The figure below shows the B=1 normalized Mathematica Alpha result.
 That result only gives one spectrum of the many Markov switching rates that may exist in nature. If we propose that B itself can vary widely, we can solve for the superstatistical RTS spectrum.
That result only gives one spectrum of the many Markov switching rates that may exist in nature. If we propose that B itself can vary widely, we can solve for the superstatistical RTS spectrum.Suppose that B ranged from close to zero to some large value R. We don't have a mean but we have these two limits as constraints. Therefore we let maximum entropy generate a uniform distribution for B.
To get the final spectrum, we essentially average the RTS spectrums over all possible intrinsic rates:
Integrate S(w|B) with respect to B from B=0 to B=R.This generates the following result
S ' (w) = arctan(R/w)/wIf R becomes large enough then the arctan converges to a constant π/2 and reduces to the 1/f spectrum if we convert w=2π*f.
S ' (f) ~ 1/fIf we reduce R in the limit, then we get a regime that has a 1/f component and a 1/f 2 above the R transition point, where it reverts back to a telegraph noise power-law.

An excellent paper by Edoardo Milotti, titled 1/f noise: a pedagogical review does a very good job of eliminating the mystery behind 1/f noise. He takes a slightly different tact but comes up with the same result that I have above.
In this review we have studied several mechanisms that produce fluctuations with a 1/f spectral density: do we have by now an "explanation" of the apparent universality of flicker noises? Do we understand 1/f noise? My impression is that there is no real mistery behind 1/f noise, that there is no real universality and that in most cases the observed 1/f noises have been explained by beautiful and mostly ad hoc models.Milotti essentially disproved Bak's theory and said that no universality stands behind the power-law, just some common sense.
From Wikipedia
I actually took a class from the professor years ago and handed in this derivation as a class assignment (we had to write on some noise topic). I thought I could get his interest up and perhaps get the paper published, but, alas, he muttered a negative with his Dutch accent.There are no simple mathematical models to create pink noise. It is usually generated by filtering white noise.
There are many theories of the origin of 1/ƒ noise. Some theories attempt to be universal, while others are applicable to only a certain type of material, such as semiconductors. Universal theories of 1/ƒ noise are still a matter of current research.
A pioneering researcher in this field was Aldert van der Ziel.
Years later, I finally get my derivation out on a blog.
As Columbo would say, just one more thing.
If the noise represents electromagnetic radiation, then one can perhaps generate an even simpler derivation. The energy of a photon is E(f)=h*f where h=Plank's constant and f is frequency. According to maximum entropy, if energy radiation remains uniform through the frequency spectrum, then we can only get this result if we apply a 1/f probability density function:
E(f) * p(E(f)) = h*f * (1/f) = constant