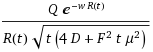The BP team apparently wanted to break up the oil up so that it could easily migrate and essentially dilute its strength within a larger volume. So instead of allowing a highly concentrated dose of oil to impact a seashore or the ocean surface, the dispersants would force the oil to remain in the ocean volume, and let the vast expanse of nature take its course. Somebody in the bureaucratic hierarchy made the calculated decision to apply dispersants as a judgment call. I can't comment on the correctness of that decision but I can expound on the topic of dispersion, which no one seems to fully understand, even in a scientific context.
As the media has forced us to listen to made up technical terms such as "top kill", "junk shot", and "top hat" which describe all sorts of wild engineering fixes, I will take a turn toward the more fundamental notions of disorder, randomness, and entropy to explain that which we cannot necessarily control. I always think that if we can understand concepts such as dispersion from first principles, we actually have a good chance of understanding how to apply it to a range of processes besides oil spill dispersal. In other words, well beyond this rather specific interpretation, we can apply the fundamentals to other topics such as green-house gases, financial market fluctuations, and oil discovery and production, amongst a host of other natural or man-made processes. Really, it is this fundamental a concept.
Background
If by the process of dispersion we want the particles to dilute as rapidly as possible, we need to somehow accelerate the rate or kinetics of the interactions. This becomes a challenge of changing the fundamental nature of the process, via a homogeneous change, or by introducing additional heterogeneous pathways that provide alternate pathways to faster kinetics. From this perspective, dispersion describes a mechanism to divergently spread-out the rates and dilute the material from its originally concentrated form. One can analogize in terms of a marathon race; the initial concentration of runners at the starting line rapidly disperses or spreads out as the faster runners move to the front and the slower runners drop to the rear. In a typical race, you see nothing homogeneous about the makeup of the runners (apart from their human qualities); the elites, competitive amateurs, and spur-of-the-moment entrants cause the dispersion. Whether we want to achieve a homogeneous dispersion or not, we have to account for the heterogeneous nature of the material. In other words, we rarely deal with pure environments so have to solve for much more than the limited variability we originally imagined. Generalizing from the rather artificial constraints of a marathon race, dispersion in other contexts (such as crystal growth or reservoir growth) results from an increase of disorder as a direct consequence of entropy and the second law of thermodynamics.
In terms of the spread in dispersion, we might often observe a tight bunching or a wide span in the results. The wider dispersion usually indicates a larger disorder, variability, or uncertainty in the characteristics -- a "fat-tail" to the statistics so to speak. So when we introduce a dispersant into the system, we add another pathway and basically remove order (or introduce disorder) into the system. Dispersion may thus not accelerate a process in a uniform manner, but instead accelerates the differences in the characteristic properties of the material. This again describes an entropic process, and we have to add energy or find exothermic pathways to fight the tide of increasing disorder.
This seems like such a simple concept, yet it rarely gets applied to most scientific discussions of the typical disordered process. Instead, particularly in an academic setting, what one usually reads amounts to pontificating about some abnormal or anomalous kind of random-walk that must occur in the system. The scientists definitely have a noble intention -- that of explaining a fat-tail phenomenon -- yet they don't want to acknowledge the most parsimonious explanation of all. They simply do not want to consider heterogeneous disorder as described by the maximum entropy principle.
 |  |
Figure 1: Difference between a classical random walk (left) and an anomalous random walk (right). The salient difference is that occasional long jumps (Levy flights) occur in the anomalous random walk. A much simpler approach admits that a heterogeneous nix of random walkers of different rates exists. This will give essentially the same observable outcome without resorting to arcane mathematical modeling.
The complicating factor in discussions about dispersion involves the intuitively related concept of diffusion and convection or drift. Diffusion also derives from the statistics of disorder and describes how particles can spontaneously spread out without a real driving force, apart from the uniform environment, for example from the thermal background. The analysis of a particle undergoing random walk leads directly to the concept of diffusion. Random walk ideas seem to intrigue mathematicians and scientists because it places the concept of diffusion into a real concrete representation. In some sense everyone can relate to the idea of a particles bouncing around, but not necessarily to the idea of a gradient in concentration.Convection and drift describe the motion of particles under an applied force, say charged particles under the influence of an electric field (Haynes-Shockley), or of solute or suspended particles under the influence of gravity (Darcy's Law). This essentially describes the typical constant velocity, akin to a terminal velocity, that we observe in a pure semiconductor (Haynes-Shockley) or a uniformly porous media (Darcy's).
Dispersion can effect both diffusion and drift, and that establishes the premise for the novel derivation that I came up with.
Breakthrough
The unification of the dispersion and diffusion concepts could have a huge influence on the way we think about practical systems, if we could only factor the mathematics describing the process. I can straightforwardly demonstrate a huge simplification assuming a single somewhat obvious premise. This involves applying the conditions of maximum entropy, by essentially maximizing disorder under known constraints or moments (i.e. mean values, etc).
The obviousness of this unifying solution contrasts with my lack of awareness of of any such similar simplification in the scientific literature. Surprisingly, I can't even confirm that anyone has really looked into the general idea. So far, I can't find any definitive work on this unification and little interest in pursuing this premise. Stating my point-of-view flatly, the result has such a comprehensive and intuitive basis that it should have a far-reaching impact on how we think about dispersion and diffusion. It just needs to gain a foothold of wider acceptance in the marketplace of ideas.
Which brings up a valid point I have heard directed my way. From my postings on TheOilDrum.com, commenters occasionally ask me why I don't publish these results in an academic setting, such as a journal article. To answer that, journals have evidently failed in this case, as I never find any serious discussion of dispersion unification. So consider that even if I submitted these ideas to a journal, it may just sit there and no one would ever apply the analysis in any future topics. This makes it an utterly useless and ultimately futile exercise. I will risk putting the results out on a blog and take my chances. A blog easily has as much archival strength, much more rapid turnaround, the potential for critiquing, and has searchability (believe it or not, googling the term "dispersive transport" yields this blog as the #3 result, out of 16,200,000). The general concepts do not apply to any specific academic discipline apart perhaps applied math, and I certainly won't consider publishing the results in that arena with out risking it disappear without a trace. Eventually, I want to place this information in a Wikipedia entry and see how that plays out. I would call it an experiment in Open Source science.
But that gets a little ahead of the significance of the current result.
The Unification of Diffusion and Drift with Dispersion
As my most recent post described, solving the Fokker-Planck equation (FPE) under maximum entropy conditions provides the fundamental unification between dispersion, diffusion and drift. For fans of Taleb and Mandelbrot, this shows directly how "thin-tail" statistics become "fat-tail" statistics without resorting to fractal arguments.
The Fokker-Planck equation shows up in a number of different disciplines. Really, anything having to do with diffusion or drift has a relation to Fokker-Planck. Thus you will see FPE show up in its various guises: Convection-Diffusion equation, Fick's Second Law of Diffusion, Darcy's Law, Navier-Stokes (kind of), Shockley's Transport Equation, Nernst-Planck; even something as seemingly unrelated as the Black-Scholes equation for finance has applicability for FPE (where the random walk occurs as fractional changes in a metric).
Because of its wide usage, the FPE tends to take the form of a hammer, where everything it applies to acts as the nail. (You don't see this more frequently than in finances, where Black-Scholes played the role of the hammer) Since the solution of FPE results in a probability distribution, it gives the impression that some degree of disorder prevails in the system under study. I find this understandable since the concept of diffusion implies an uncertainty exactly like a random walk shows uncertainty. In other words, no two outcomes will turn out exactly the same. Yet, in mathematical terms, the measurable value associated with diffusion, the diffusion constant D, has a fixed value for random motion in a homogeneous environment. When the parameters actually change, you enter in the world of stochastic differential equations; I won't descend to deeply into this area, only to apply this as a basic concept. The diffusion and mobility parameters have a huge variability that we have yet adequately accounted for in many disordered systems.
For that reason, the FP equation really applies to ordered systems that we can characterize well. Not surprisingly the ordinary solution to FPE gives rise to the conventional ideas of normal statistics and thin-tails.
So for phenomenon that appear to depart from conventional normal diffusion (the so-called anomalous diffusion) we have two distinct camps and corresponding solution paths to choose from. The prevailing wisdom suggests that an entirely different kind of random walk occurs (Camp 1). No longer does the normal diffusion apply, giving rise to normal statistics; instead we get the statistics of fat-tails and random walk trajectories called Levy flights to concretely describe the situation (see Figure 1). The mathematics quickly gets complicated here and most of the results get cast into heuristic power-laws. It takes a leap of faith to follow these arguments.
The question comes down to whether we wish to ascribe anomalous diffusion as a strange kind of random walk (Camp 1) or simply suggest that heterogeneity in diffusional and drift properties adequately describes the situation (Camp 2). I take the stand in the latter category and stand pretty much alone in this regard. Find some academic research article on anything related to anomalous diffusion and very few will accept the most parsimonious explanation -- that a range of diffusion constants and mobilities explain the results. Instead the researcher will punt and declare that some abstract Levy flight describes the motion. Above all I would rather think in practical terms, and simple variability has a very pragmatic appeal to it.
I went through the derivation of the dispersive FPE solution for a disordered semiconductor in the last post, and want to generalize it here. This makes it especially applicable to notions of transport physical transport of material in porous matter. This would include the motion of oil underground, CO2 in the air, and perhaps even spilled oil at sea.
In the one-dimensional model of applying an impulse function of material, the concentration n will disperse according to the following equation:
n(x, z) = (z + sqrt(zL + z^2)/sqrt(zL + z^2)*exp(-2x/(z + sqrt(zL + z^2))The term z takes the place of a time-scaled distance, which can speed up or slow down under the influence of a force F (i.e. gravity, or electric field for a charged particle). The characteristic distance L represents the effect of the stochastic force β (aka Boltzmann's constant) and ties in the diffusional aspects of the system. The specific parameterization of the exponential results in the fat-tail observed.
where
z= μFt
L = β/F
In the past, I had never gone through the trouble of solving the FPE, simply because intuition would suggest that the dispersive envelope would cancel out most of the details of the diffusion term. In the dispersive transport model that I originally conceived, the dispersion would at most follow the leading wavefront of the drifting diffusional field as "sqrt(Lz+z^2)" as described here or as "sqrt(Lz)+z" here.
I estimated that the diffusion term would follow as the square root of time according to Fick's first law and that drift would follow time linearly, with only an idea of the qualitative superposition of the terms in my mind.
As one might expect, the actual entropic FPE solution borrowed from a little of each of my estimates, essentially averaging between the two:
(z + sqrt(zL + z^2))/2So the solution to the dispersive FPE form for a disordered system turns out entirely intuitive , and one can almost generate the result from inspection. The difference between the original entropic dispersion derivation and the full FPE treatment amounts to a bit of pre-factor bookkeeping in the first equation above. You can see this by comparing the two approaches for the case of L=1 and unity width for the dispersive transport current model.
Figure 2: Differences between the original entropic dispersive model and the fully quantified FPE solution will converge as L gets smaller.Dispersive Transport in Porous Media.
The above solved equations can actually apply directly as solutions to Darcy's law when it comes to describing the flow of material in a disordered porous media. I suppose this will irk the petroleum engineers, hydrologists, and geologists out there who have long sought the solution to this particular problem.
Yet we should not act surprised by this result. The actions of multiple processes acting concurrently on a mobile material will generally result in a universal form governed by maximum entropy. It doesn't matter if we model carriers in a semiconductor or particles in a medium, the result will largely look the same. In a hydraulic conductivity experiment, Lange treated the breakthrough curve of a trace element through a natural catchment as a FPE convection-dispersion model, and came up with the same results independent of the fractionation of the media.
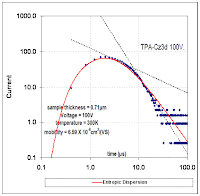
By applying the simple dispersion model (blue curve below) to Lange's results, one sees that an excellent fit results with the fat-tail exactly following the hyperbolic decline that reservoir engineers often see in long-term flow behavior. This could includes the time dependent emptying of the currently leaking deep sea Gulf reservoir!
Figure 3: Breakthrough curve of a traced material showing results from an entropic dispersion model in blue.
Moreover, the amount of diffusion that occurs appears quite minimal. Adding a greater proportion of diffusion by increasing L does not improve the fit of the curve (see the chart to the right). Just as in the semiconductor case, the shape has a significant meaning when analyzed from the perspective of maximum entropy.Nothing complicated about this other than admitting to the fact that heterogeneous disordered systems appear everywhere and we have to use the right models to characterize their behavior.
The details of this experiment are described in the following papers:
- D.Haag and M.Kaupenjohann, Biogeochemical Models in the Environmental Sciences: The Dynamical System Paradigm and the Role of Simulation Modeling
- H. Lange, Are Ecosystems Dynamical Systems?
Still the work of modeling the physical process alone has enormous value as Haag and Kaupenjohann point out:
We need to really take up the charge on this as our future depends on understanding the role of entropy in nature. For too long, we have not shown the intellectual curiosity to model how much oil we have underground, what size distribution the reservoirs take, and how fast that they can epmty, even though some perfectly acceptable models can describe this statistically, using dispersion no less!Despite not being a ‘real’ thing, "a model may resonate with nature" (Oreskes et al. 1994) and thus has heuristic value, particular to guide further study. Corresponding to the heuristic function, Joergensen (1995) claims that models can be employed to reveal ecosystem properties and to examine different ecological theories. Models can be asked scientific questions about properties. According to Joergensen (1994), examples for ecosystem properties found by the use of models as synthesizing tools are the significance of indirect effects, the existence of a hierarchy, and the ‘soft’ character of ecosystems. However, we agree with Oreskes et al. (1994) who regard models as "most useful when they are used to challenge existing formulations rather than to validate or verify them". Models, as ‘sets of hypotheses’, may reveal deficiencies in hypotheses and the way biogeochemical systems are observed. Moreover, models frequently identify lacunae in observations and places where data are missing (Yaalon 1994).
As an instrument of synthesis (Rastetter 1996), models are invaluable. They are a good way to summarize an individual research project (Yaalon 1994) and they are capable of holding together multidisciplinary knowledge and perspectives on complex systems (Patten 1994).
While models as a product may have heuristic value, we would like to emphasize also the role of the modeling process: "[…] one of the most valuable benefits of modeling is the process itself. These benefits accrue only to participants and seem unrelated to the character of the model produced" (Patten 1994). Model building is a subjective procedure, in which every step requires judgment and decisions, making model development ‘half science, half art’ and a matter of experience (Hoffmann 1997, Hornung 1996). Thus modeling is a learning process in which modelers are forced to make explicit their notions about the modeled system and in which they learn how the analytically isolated components of a system can be ‘glued’ (Paton 1997). As modeling mostly takes place in groups, modeling and the synthesis of knowledge has to be envisaged as a dynamic communication process, in which criteria of relevance, the meaning of terms, the underlying concepts and theories, and so forth are negotiated. Model making may thus become a catalyst of interdisciplinary communication.
In the assessment of environmental risks, however, an exclusively scientific modeling process is not sufficient, as technical-scientific approaches to ‘post-normal’ risks are unsatisfactory (Rosa 1998) and as the predictive capacity and operational validity of models (e.g. for scenario computation) is in doubt. The post-normal science approach (Funtowicz & Ravetz 1991, 1992, 1993) takes account of the stakes and values involved in environmental decision making. Following a ‘post-normal’ agenda, model development and model validation for risk assessment should become a trans-scientific (communication) task, in which "extended peer communities" participate and in which non-equivalent descriptions of complex systems are made explicit, negotiated, and synthesized. In current modeling practice, however, models are highly opaque and can rarely be penetrated even by other scientists (Oreskes, personal communication). As objects of communication, models still are closed systems and black boxes.
Now that the Macondo oil has discovered an escape hatch and has gone disordered on us and will go who-knows-where, it seems we can really make some headway in our common understanding. Nothing like having your feet in the fire.
